Clebsch graph
| Clebsch graph | |
|---|---|
| Named after | Alfred Clebsch |
| Vertices | 16 |
| Edges | 40 |
| Radius | 2 |
| Diameter | 2 |
| Girth | 4 |
| Automorphisms | 1920 |
| Chromatic number | 4[1] |
| Chromatic index | 5 |
| Properties | Strongly regular Hamiltonian Triangle-free Cayley graph Vertex-transitive Edge-transitive Distance-transitive. |
In the mathematical field of graph theory, the Clebsch graph[1][2] is an undirected graph with 16 vertices and 40 edges. It is named after Alfred Clebsch, a German mathematician who discovered it in 1868. It is also known as the Greenwood–Gleason graph after the work of Robert M. Greenwood and Andrew M. Gleason (1955), who used it to evaluate the Ramsey number R(3,3,3) = 17.[3][4][5]
Contents |
Construction
This graph is equivalent to the order-5 folded cube graph. It may be constructed by adding edges between opposite pairs of vertices in a 4-dimensional hypercube graph. (In an n-dimensional hypercube, a pair of vertices are opposite if the shortest path between them has n edges.) Alternatively, it can be formed from a 5-dimensional hypercube graph by identifying together (or contracting) every opposite pair of vertices.
Another construction, leading to the same graph, is to create a vertex for each element of the finite field GF(16), and connect two vertices by an edge whenever the difference between the corresponding two field elements is a perfect cube.[6]
Properties
The Clebsch graph is a strongly regular graph of degree 5 with parameters 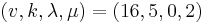 .[7][8] Its complement is also a strongly regular graph.[1][4]
.[7][8] Its complement is also a strongly regular graph.[1][4]
The graph is hamiltonian, non planar and non eulerian. It is also both 5-vertex-connected and 5-edge-connected.
The subgraph that is induced by the ten non-neighbors of any vertex in the Clebsch graph forms an isomorphic copy of the Petersen graph.
The edges of the complete graph K16 may be partitioned into three disjoint copies of the Clebsch graph. Because the Clebsch graph is a triangle-free graph, this shows that there is a triangle-free three-coloring of the edges of K16; that is, that the Ramsey number R(3,3,3) describing the minimum number of vertices in a complete graph without a triangle-free three-coloring is at least 17. Greenwood & Gleason (1955) used this construction as part of their proof that R(3,3,3) = 17.[5][9]
The Clebsch graph is the Keller graph of dimension two, part of a family of graphs used to find tilings of high-dimensional Euclidean spaces by hypercubes no two of which meet face-to-face.
Algebraic properties
The characteristic polynomial of the Clebsch graph is 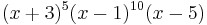 . Therefore the Clebsch graph is an integral graph: its spectrum consists entirely of integers.[4] The Clebsch graph is the only graph with this characteristic polynomial, making it a graph determined by its spectrum.
. Therefore the Clebsch graph is an integral graph: its spectrum consists entirely of integers.[4] The Clebsch graph is the only graph with this characteristic polynomial, making it a graph determined by its spectrum.
The Clebsch graph is a Cayley graph with an automorphism group of order 1920, isomorphic to the Coxeter group 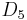 . As a Cayley graph, its automorphism group acts transitively on its vertices, making it vertex transitive. In fact, it is arc transitive, hence edge transitive and distance transitive.
. As a Cayley graph, its automorphism group acts transitively on its vertices, making it vertex transitive. In fact, it is arc transitive, hence edge transitive and distance transitive.
Gallery
References
- ^ a b c Weisstein, Eric W.. "Clebsch Graph.". From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/ClebschGraph.html. Retrieved 2009-08-13.
- ^ Brouwer et al. (1989) use name Clebsch graph for a different, but related graph.
- ^ Clebsch, A. (1868), "Ueber die Flächen vierter Ordnung, welche eine Doppelcurve zweiten Grades besitzen", J. für Math. 69: 142–184.
- ^ a b c The Clebsch Graph on Bill Cherowitzo's home page
- ^ a b Greenwood, R. E.; Gleason, A. M. (1955), "Combinatorial relations and chromatic graphs", Canadian Journal of Mathematics 7: 1–7, doi:10.4153/CJM-1955-001-4, MR0067467.
- ^ De Clerck, Frank (1997). "Constructions and Characterizations of (Semi)partial Geometries". p. 6. http://cage.ugent.be/~fdc/potenza.ps.
- ^ Godsil, C.D. (1995). "Problems in algebraic combinatorics". Electron. J. Combin. 2: 3. http://www.combinatorics.org/Volume_2/PDFFiles/v2i1f1.pdf. Retrieved 2009-08-13.
- ^ Peter J. Cameron Strongly regular graphs on DesignTheory.org, 2001
- ^ Sun, Hugo S.; Cohen, M. E. (1984), "An easy proof of the Greenwood-Gleason evaluation of the Ramsey number R(3,3,3)", The Fibonacci Quarterly 22 (3): 235–238, MR765316, http://www.fq.math.ca/Scanned/22-3/sun.pdf.